Mathematics In Robotics
- Siya Gupta
- Aug 22, 2024
- 3 min read
Updated: Nov 23, 2024
1. Forward Kinematics
Equation:

Explanation:
Forward kinematics calculates the end effector's position and orientation by combining the effects of all joints' movements in a robotic arm. Each joint iii contributes to the overall position through a transformation matrix Ti, which includes rotation and translation components.
Transformation Matrix (Ti): Each matrix represents the joint’s contribution to the arm's overall position. It is derived from the Denavit-Hartenberg parameters or other coordinate systems. For example, a typical transformation matrix for a joint might look like this:

Where θi is the joint angle, αi is the link twist, ai is the link length, and di is the link offset.
Application: Forward kinematics is used in robotic arms for tasks requiring precise tool placement. For instance, in automated assembly lines, it calculates the exact position of the end effector to pick up or place objects accurately.
2. Inverse Kinematics
Equation:
Pdesired=Tdesired
Explanation:
Inverse kinematics determines the necessary joint angles to achieve a desired position of the end effector. Given a target position Pdesired, the challenge is to compute the joint angles θ that will place the end effector exactly at Pdesired. This often involves solving nonlinear equations and may require iterative numerical methods due to the complexity of the equations.
Application: Inverse kinematics is crucial in robotic arms used for tasks such as assembling electronic components or performing surgery. For example, in a surgical robot, inverse kinematics calculates the precise angles for the robotic arm to reach a specific location inside a patient's body.
3. Control Theory
Equation (PID Controller):
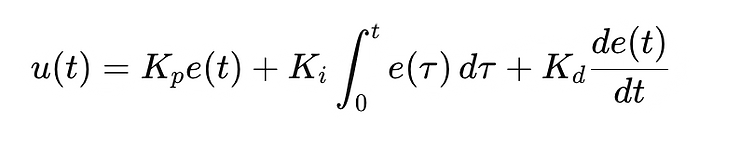
Explanation:
The PID controller adjusts the control input u(t)u(t)u(t) to minimize the error e(t)e(t)e(t) between the desired and actual positions. The equation includes:
Proportional Term ( Kpe(t) ): Directly proportional to the current error. It helps reduce the overall error quickly.
Integral Term ( Ki∫0te(τ) dτ ): Accumulates past errors to eliminate residual steady-state error.
Derivative Term ( Kd(de(t)/dt ): Predicts future error based on the rate of change, helping to dampen oscillations and improve stability.
Application: PID controllers are used in various robotic applications such as drone flight control, where precise adjustments are needed to maintain stable flight and trajectory, or in industrial robots for maintaining consistent speed and position during tasks like welding.
4. Linear Algebra
Equation (Rotation Matrix):

Explanation:
The rotation matrix R(θ) describes how an object rotates in 2D space by an angle θ. It helps in transforming coordinates and calculating the new orientation of parts of a robot.
Application: Rotation matrices are used in robotics for tasks requiring orientation adjustments, such as rotating a robotic arm’s end effector to align with a specific orientation for tasks like painting or drilling at precise angles.
5. Kalman Filters
Equation:

Explanation:
The Kalman filter estimates the state xk∣k of a system, incorporating measurements zk and adjusting predictions based on the measurement matrix Hk and Kalman gain Kk. It helps to filter out noise and provide accurate state estimations.
Application: In autonomous vehicles, Kalman filters are used for sensor fusion, combining data from GPS, radar, and cameras to accurately estimate the vehicle's position and velocity, thus enhancing navigation and obstacle avoidance capabilities.
6. Optimization
Equation (Gradient Descent):

Explanation:
Gradient descent optimizes parameters θ by iteratively adjusting them in the direction of the steepest decrease of the cost function J. The learning rate α\alphaα controls the size of the adjustment, and ∇J(θk) represents the gradient of the cost function with respect to the parameters.
Application: Optimization algorithms are used in machine learning for robotic systems to fine-tune models for tasks like object recognition or path planning. For example, in robotic grasping, optimization helps in learning the best grasping strategies from data to improve the accuracy and efficiency of picking up objects.
These equations and their applications form the bedrock of modern robotics, enabling robots to perform complex tasks with precision, efficiency, and adaptability. Each mathematical principle contributes to making robots smarter, more capable, and more versatile in their operations.
Comentarios